スピノルとはで取り上げたのはローレンツ変換のスピノルだったが、スピノルを詳細に見ていくために、まずは最も簡単な3次元回転のスピノルを取り上げたい。
ベクトルの行列表示
3次元回転では、計量$\delta_{ij}$が保存される。($\delta_{ij}$はクロネッカーのデルタである。)この計量の下で実ベクトル$\vec{x}=\sum_{i=1}^{3}\vec{e}_{i}x^i$同士の内積をとる。それは、
\begin{align*}
\abs{\vec{x}}^2=\sum_{i,j=1}^{3}\delta_{ij}x^i x^j
=\mqty(x^1& x^2 & x^3)
\mqty(1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1)
\mqty(x^1 \\ x^2 \\ x^3)
\end{align*}
であり、2次形式である。これを、
\begin{align}
\abs{\vec{x}}^2=\qty(\gamma_1 x^1+\gamma_2 x^2+\gamma_3 x^3)^2\label{1}
\end{align}
という、1次形式の2乗の形で書き換えることを考える。これらの係数$\gamma_i$がみたす条件を求めよう。\eqref{1}式の右辺を展開すると、
\begin{align*}
&\qty(\gamma_1 x^1+\gamma_2 x^2+\gamma_3 x^3)^2\\
&=\gamma_i\gamma_jx^ix^j\\
&=\qty(\gamma_1)^2\qty(x^1)^2
+\qty(\gamma_2)^2\qty(x^2)^2
+\qty(\gamma_3)^2\qty(x^3)^2\\
&\quad+\qty(\gamma_1\gamma_2+\gamma_2\gamma_1)x^1x^2
+\qty(\gamma_2\gamma_3+\gamma_3\gamma_2)x^2x^3
+\qty(\gamma_3\gamma_1+\gamma_1\gamma_3)x^3x^1
\end{align*}
となるから、$\gamma_i$は
\begin{align}
\qty{\gamma_i,\gamma_j}=2\delta_{ij}\label{gamma mat def}
\end{align}
をみたさなければならないことが分かる。このような係数$\gamma_i$は、明らかに数では存在し得ず、何らかの行列で表される。\eqref{gamma mat def}式の反交換関係をみたす3つの行列を、3次元回転のガンマ行列と呼ぶ。この3つのガンマ行列を具体的に求めてみよう。
まず、行列の成分表示を持ち出さなくとも得られる性質を挙げておこう。
- ガンマ行列はトレースレスである。
<証明>
$i\neq j$とすると、
\begin{align*}
\tr[\underbrace{\qty{\gamma_i,\gamma_j}}_{=\mathbf{0}}\gamma_j]
&=\tr[\gamma_i\gamma_j\gamma_j+\gamma_j\gamma_i\gamma_j]\\
0&=2\tr[\gamma_i]
\end{align*}
である。(ただし、$j$についての和は取っていない。)
これより、
\begin{align*}
\tr[\gamma_i]=0
\end{align*}
である。
<証明終> - ガンマ行列の次元は偶数である。
<証明>
ガンマ行列は$\qty(\gamma_i)^2=\mathbf{1}$をみたすから、固有値は$\pm 1$である。ガンマ行列はトレースレスだから、その固有値$+1$と$-1$は同数だけある。したがって、ガンマ行列の次元は偶数でしかありえない。
<証明終>
ガンマ行列の具体的な表式を最も簡単な形で求めるため、さらに以下のエルミート条件を課してみる1:
\begin{align*}
\gamma_i^{\dagger}=\gamma_i.
\end{align*}
この条件を課したガンマ行列を、本ブログではエルミート表示と呼ぶことにする。
以上の事項からガンマ行列の表式を求めよう。サイズは考え得る限り最も小さい$2\times 2$行列とする:
\begin{align*}
\gamma_i=\mqty(\alpha & \beta \\ \gamma & \delta).\quad\qty(\alpha,\beta,\gamma,\delta\in\mathbb{C})
\end{align*}
$\qty(\gamma_i)^{\dagger}=\gamma_i$より$\alpha^*=\alpha,\ \delta^*=\delta,\ \beta^*=\gamma$であり、さらに$\tr[\gamma_i]=0$より$\delta=-\alpha$だから、これは、
\begin{align*}
\gamma_i=\mqty(a & b-ic \\ b+ic & -a) \quad\qty(a,b,c\in\mathbb{R})
\end{align*}
と絞り込める。
したがって、
\begin{align*}
\gamma_j=\mqty(a’ & b’-ic’ \\ b’+ic’ & -a’) \quad\qty(a’,b’,c’\in\mathbb{R})
\end{align*}
とすると、
\begin{align*}
\qty{\gamma_i,\gamma_j}
&=\qty{\mqty(a & b-ic \\ b+ic & -a),\mqty(a’ & b’-ic’ \\ b’+ic’ & -a’)}\\
&=2(aa’+bb’+cc’)\mqty(1 & 0 \\ 0 & 1)
\end{align*}
となるから、例えば$(a,b,c)=(1,0,0),(0,1,0),(0,0,1)$となるように3つの行列を定めれば、$\qty{\gamma_i,\gamma_j}=2\delta_{ij}\mathbf{1}$をみたす$2\times 2$行列が得られる。そのように定めた行列は、
\begin{align*}
\gamma_1=\mqty(0 & 1 \\ 1 & 0),\quad \gamma_2=\mqty(0 & -i \\ i & 0),\quad \gamma_3=\mqty(1 & 0 \\ 0 & -1)
\end{align*}
である。こうして、3つのガンマ行列が求められた。これらは特にパウリ行列とよばれ、通常$\sigma_i\equiv\gamma_i$と書かれる。
以上より、3次元ベクトル成分$x=\mqty(x^1 \\ x^2 \\ x^3)$は、
\begin{align}
\slashed{x}
\equiv\sum_{i=1}^{3}\sigma_ix^i
=\mqty(x^3 & x^1-ix^2 \\ x^1+ix^2 & -x^3)\label{slashed vec}
\end{align}
と、行列としても表現できることが分かる。
スピノルの定義
ここで、パウリ行列のいくつかの積を取ってできる行列を列挙してみよう。パウリ行列の性質を使えば、そのような行列のうち、互いに独立(互いに定数倍の関係にない)なものは以下の4つである:
\begin{align}
\mathbf{1}_2,\ \sigma_1,\ \sigma_2,\ \sigma_3.\label{bases}
\end{align}
これらの行列が作用するベクトル空間の元を3次元回転のスピノルという。行列が$2\times 2$だから、3次元回転のスピノル成分は2成分の数ベクトルとして書ける2。以下、スピノルを半割れ矢印によって$\overset{\rightharpoondown}{\xi}$と表記する。
スピノルの成分や基底もベクトルの場合と同じように反変・共変を考えることができるし、スピノル同士の内積も与えることができる。それを以下のように書く:
\begin{align*}
&\spn{\xi}=\sum_{a=1}^2\spn{e}_a\xi^a\quad(\text{共変基底と反変成分の組}),\\ &\spn{\zeta}=\sum_{a=1}^2\zeta_a\spn{e}^a\quad(\text{共変成分と反変基底の組}),\\
&\spn{\zeta}\cdot\spn{\xi}=\sum_{a=1}^2\zeta_a\xi^a\quad(\text{スピノル同士の内積}).
\end{align*}
また、スピノル成分の組を数ベクトルとして表記することもある。例えば、$\spn{\xi},\spn{\zeta}$の成分の組$\xi,\zeta$はそれぞれ
\begin{align*}
\xi=\mqty(\xi^1 \\ \xi^2),\quad
\zeta=\mqty(\zeta_1 & \zeta_2)
\end{align*}
と書く。
スピノル成分とベクトル成分の関係
ベクトル成分をスピノル成分で表す
ベクトル成分がスピノル成分によってどのように表されるかみてみよう。そのために、ベクトルの行列表示(\eqref{slashed vec}式)を考える。任意の$2\times 2$行列は4つの成分をもつ。そして、線形独立な基底となる$2\times 2$行列が4つあれば、それらの線形結合によって任意の$2\times 2$行列を表現できる。今、\eqref{bases}における4つの行列の線形結合として
\begin{align*}
a\mathbf{1}_2+\sigma_ix^i =\mqty(a+x^3 & x^1-ix^2 \\ x^1+ix^2 & a-x^3)
\end{align*}
という行列を考え、この行列式が0となるように$a$を調整してみる。すると、
\begin{align*}
\det\mqty(a+x^3 & x^1-ix^2 \\ x^1+ix^2 & a-x^3)
=a^2-\underbrace{\qty((x^1)^2+(x^2)^2+(x^3)^2)}_{=r^2}
=a^2-r^2
\end{align*}
より、$a=\pm r$ならばこの行列式は$0$となる。ここでは$a=r$と選ぼう。行列式が0である行列は、2つのベクトルのテンソル積として表せる3から、スピノル$\spn{\xi}=\sum_{a=1}^2\spn{e}_a\xi^a,\ \spn{\zeta}=\sum_{a=1}^2\zeta_a\spn{e}^a$の成分$\xi=\mqty(\xi^1 \\ \xi^2)\in\mathbb{C}^2\ \zeta=\mqty(\zeta_1 & \zeta_2)\in\mathbb{C}^2$を用いて、
\begin{align}
\xi\zeta=\frac{1}{2}\qty(r\mathbf{1}_2+\sigma_ix^i)\label{4}
\end{align}
と書ける4。
$x^i$を$\xi,\zeta$で表すには、\eqref{4}式に$\sigma^{i}\equiv\delta^{ij}\sigma_{i}=\sigma_{i}$をかけてトレースを取ればよい:
\begin{align*}
\tr\qty[\xi\zeta\sigma^i]
&=\frac{1}{2}\tr\qty[\cancel{r\mathbf{1}_2\sigma^i}+\sigma_jx^j\sigma^i]\\
&=\frac{1}{2}\tr\qty[\qty(\delta_{j}^{i}\mathbf{1}_2+\cancel{i\varepsilon_{j}{}^{ik}\sigma_k}) x^j]\\
&=\frac{1}{2}2\delta^{i}_{j}x^j\\
&=x^i.
\end{align*}
したがって、
\begin{align}
x^i=\tr\qty[\xi\zeta\sigma^i]=\zeta\sigma^i\xi\label{5}
\end{align}
と書ける。
スピノル成分をベクトル成分で表す
逆にスピノル成分をベクトル成分で表すこともできる。
まず、\eqref{5}式両辺の自由度について述べておく。左辺の自由度は3であり、右辺の自由度は8もある。ベクトル成分からスピノル成分を求めたいときは、これでは冗長である。そこで、$\zeta=\xi^{\dag}$とすることで自由度を4に低減させる56。
この置き換えの下で\eqref{5}式を具体的に書けば
\begin{align}
x^1&=\mqty(\xi^{1*} & \xi^{2*})\mqty(0 & 1 \\ 1 & 0)\mqty(\xi^1 \\ \xi^2)
=\xi^{1*}\xi^2+\xi^{2*}\xi^1\label{q}\\
x^2&=\mqty(\xi^{1*} & \xi^{2*})\mqty(0 & -i \\ i & 0)\mqty(\xi^1 \\ \xi^2)
=-i\xi^{1*}\xi^2+i\xi^{2*}\xi^1\label{w}\\
x^3&=\mqty(\xi^{1*} & \xi^{2*})\mqty(1 & 0 \\ 0 & -1)\mqty(\xi^1 \\ \xi^2)
=\abs{\xi^1}^2-\abs{\xi^2}^2\label{e}
\end{align}
である。
加えて、$\xi\xi^{\dag}$に$\mathbf{1}_2$をかけてトレースを取ると、
\begin{align*}
\tr\qty[\xi\xi^{\dag}\mathbf{1}_2]
=\frac{1}{2}\tr\qty[r\mathbf{1}_2\mathbf{1}_2+\cancel{\sigma_jx^j\mathbf{1}_2}]
=\frac{1}{2}2r
=r
\end{align*}
となるから、
\begin{align}
r=\mqty(\xi^{1*} & \xi^{2*})\mqty(1 & 0 \\ 0 & 1)\mqty(\xi^1 \\ \xi^2)
=\abs{\xi^1}^2+\abs{\xi^2}^2\label{rr}
\end{align}
である。
$\xi$の成分を$x^1,x^2,x^3,r$で表すには、極座標表示
\begin{align*}
x^1=r\sin\theta\cos\varphi,\quad x^2=r\sin\theta\sin\varphi,\quad x^3=r\cos\theta
\end{align*}
を用いるのがよい。
まず、\eqref{e}式と\eqref{rr}式を辺々足すと、
\begin{align*}
\eqref{e}\text{式}+\eqref{rr}\text{式}:
2\abs{\xi^1}^2&=x^3+r\\
&=r(1+\cos\theta)\\
&=r2\cos^2\frac{\theta}{2}
\end{align*}
だから、
\begin{align}
\xi^1&=\sqrt{r}\cos\frac{\theta}{2}e^{i\Phi}
\label{aa1}\quad(\text{$\Phi$は任意の実数})
\end{align}
を得る。また、\eqref{e}式と\eqref{rr}式を辺々引くと、
\begin{align*}
\eqref{rr}\text{式}-\eqref{e}\text{式}:
2\abs{\xi^2}^2
&=r-x^3\\
&=r\qty(1-\cos\theta)\\
&=r2\sin^2\frac{\theta}{2}
\end{align*}
だから、
\begin{align}
\xi^2&=\sqrt{r}\sin\frac{\theta}{2}e^{i\Phi’}
\label{aa2}\quad(\text{$\Phi’$は任意の実数})
\end{align}
である。
次に、
\begin{align*}
x^1+ix^2&=\xi^{1*}\xi^2+\xi^{2*}\xi^1+\xi^{1*}\xi^2-\xi^{2*}\xi^1=2\xi^{1*}\xi^2\\ x^1+ix^2&=r\sin\theta(\cos\varphi+i\sin\varphi)=r\sin\theta e^{i\varphi}
\end{align*}
の2式を比較して、
\begin{align}
\xi^{1*}\xi^2=\frac{1}{2}r\sin\theta e^{i\varphi}\label{bbb}
\end{align}
を得る。一方、
\begin{align*}
(\eqref{aa1}\text{式})^*\times\eqref{aa2}\text{式}: \xi^{1*}\xi^2
&=r\cos\frac{\theta}{2}\sin\frac{\theta}{2}e^{i(-\Phi+\Phi’)}\\
&=\frac{1}{2}r\sin\theta e^{i(-\Phi+\Phi’)}
\end{align*}
だから、これと\eqref{bbb}式を比較して
\begin{align}
-\Phi+\Phi’=\varphi
\end{align}
が分かる。
ここで、
\begin{align*}
\Phi=-\frac{1}{2}\qty(\varphi+\gamma),\quad
\Phi’=\frac{1}{2}\qty(\varphi-\gamma)\\
(\text{$\gamma$は$0\leq\gamma <4\pi$をみたす任意の実数})
\end{align*}
と、新たな自由度$\gamma$を導入してみると7、最終的に
\begin{align*}
\xi^1&=\sqrt{r}\cos\frac{\theta}{2}e^{-\frac{i}{2}\qty(\varphi+\gamma)}\\
\xi^2&=\sqrt{r}\sin\frac{\theta}{2}e^{\frac{i}{2}\qty(\varphi-\gamma)}
\end{align*}
と書け、$\xi$の成分の具体形が得られた。
スピノル成分の表式に任意の実数$\gamma$があるのが不思議だが、これは3つの自由度$x^1,x^2,x^3$を(複素数の範囲で)4つの自由度を持つ$\xi$で表したために生じた任意性である。$\gamma$はスピノル成分の位相として登場しているため、位相の不定性に対応していると理解できる。ただ、$x^i=\xi^{\dag}\sigma^i\xi$の表式から分かるとおり、ベクトルの成分を表すときには位相は相殺して現れないため、この不定性については特に取り決める必要がない。
また、$\xi$の表式では、角度$\theta,\varphi$は必ず$\frac{1}{2}$倍された状態で登場する。つまり、ベクトルを1回転させたとき、対応するスピノルは半回転しかしないということである。これは\eqref{5}式からも納得できる。即ち、$x^i=\xi^{\dag}\sigma^i\xi$において、2つのスピノル$\xi,\xi^{\dag}$の回転を合わせてベクトル$x$の回転を表すのだから、スピノル1個当たりの回転はベクトルの半分になると理解できる。その意味で、スピノルは「ベクトルの平方根」のようなものだと捉えられる。
スピノルの幾何学的解釈
3次元回転のスピノルは、ステレオグラフ射影と呼ばれる方法によって、幾何学的に理解できる。
単位球が図1のように置かれているとする。単位球の南極$S=(0,0,-1)$と単位球面上の任意の点$P=(x^1,x^2,x^3)$を通る直線を$l$とし、直線$l$が$x,y$平面と交わる点の$x,y$座標を$(x,y)$とする。
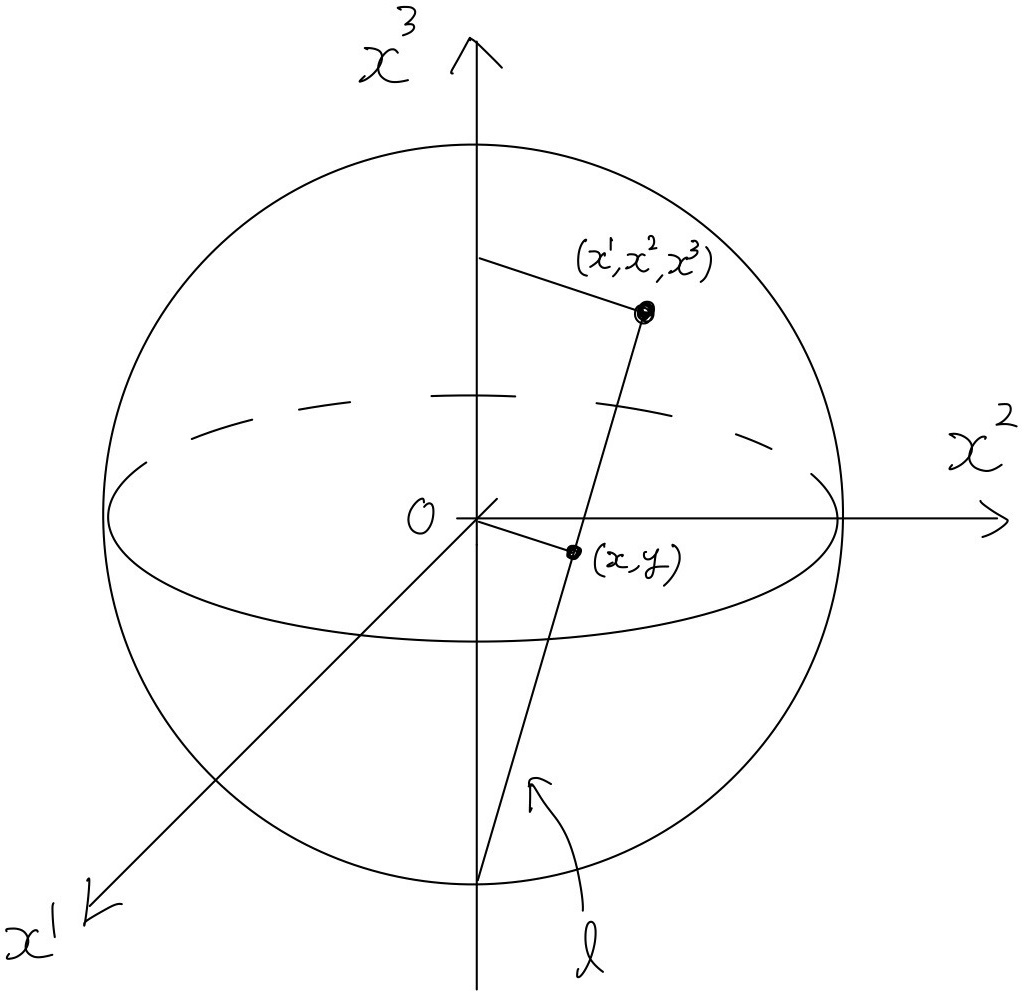
図1 単位球と座標
この図における$x,y$平面を複素平面とみなし、座標$(x,y)$を複素数$\zeta=x+iy$に対応させる。この対応関係を具体的に求めてみよう。
まず、球面の方程式と直線$l$の方程式は、それぞれ
\begin{align}
&(x^1)^2+(x^2)^2+(x^3)^2=1\label{s1}\\
&\frac{x^1}{x}=\frac{x^2}{y}=\frac{x^3+1}{1}\label{s2}
\end{align}
である。\eqref{s1}式に\eqref{s2}式を代入すると、
\begin{align*}
(x^1)^2+\qty(\frac{y}{x}x^1)^2+\qty(\frac{x^1}{x}-1)^2&=1\\
(x^1)^2+\qty(\frac{y}{x})^2 (x^1)^2+\frac{1}{x^2}(x^1)^2-2\frac{x^1}{x}+1&=1\\
(x^1)^2\qty(1+\frac{y^2}{x^2}+\frac{1}{x^2})-2\frac{x^1}{x}&=0\\
x^1\qty(x^1\frac{x^2+y^2+1}{x^2}-\frac{2}{x})&=0\\
\qty(\text{$x^1\neq 0$とする。$\abs{\zeta}^2=x^2+y^2$を使う。})\\
x^1\frac{\abs{\zeta}^2+1}{x^2}-\frac{2}{x}&=0\\
\end{align*}
だから、
\begin{align}
x^1=\frac{2x}{1+\abs{\zeta}^2}\label{s3}
\end{align}
が得られる。全く同様にして、
\begin{align}
x^2=\frac{2y}{1+\abs{\zeta}^2}\label{s4}
\end{align}
が得られる。\eqref{s3}式と\eqref{s4}式を\eqref{s1}式に代入して、
\begin{align*}
x^3=\frac{1-\abs{\zeta}^2}{1+\abs{\zeta}^2}\label{s5}
\end{align*}
が得られる。
このままでは南極が$\abs{\zeta}=\infty$となって不便だから、これを回避するために$\zeta=\frac{\eta^2}{\eta^1}\ (\eta^2,\eta^1\in \mathbb{C})$とおく。すると、
\begin{align*}
\zeta
&\equiv x^1+ix^2
=2\frac{x+iy}{1+\abs{\zeta}^2}
=\frac{2\zeta}{1+\abs{\zeta}^2}
=\frac{2\frac{\eta^2}{\eta^1}}{1+\frac{\abs{\eta^2}^2}{\abs{\eta^1}^2}}
=\frac{2\eta^2\eta^{1*}}{\abs{\eta^1}^2+\abs{\eta^2}^2}
\end{align*}
となるから、これより、
\begin{align*}
x^1 &=\Re(\zeta’) =\frac{1}{2}\qty(\zeta’+\zeta’^*)
=\frac{\eta^2\eta^{1*}+\eta^{2*}\eta^1}{\abs{\eta^1}^2+\abs{\eta^2}^2}\\
x^2
&=\Im(\zeta’)
=\frac{1}{2i}\qty(\zeta’-\zeta’^*) =\frac{1}{i}\frac{\eta^2\eta^{1*}-\eta^{2*}\eta^1}{\abs{\eta^1}^2+\abs{\eta^2}^2}\\
x^3&=\frac{1-\frac{\abs{\eta^2}^2}{\abs{\eta^1}^2}}{1+\frac{\abs{\eta^2}^2}{\abs{\eta^1}^2}}
=\frac{\abs{\eta^1}^2-\abs{\eta^2}^2}{\abs{\eta^1}^2+\abs{\eta^2}^2}
\end{align*}
となり、南極は$\eta^1=0,\eta^2\neq 0$に対応する。
こうして、3次元回転において、3次元の座標$(x^1,x^2,x^3)$を2つの座標$(\eta^1,\eta^2)$に対応づけられることが確認できた。ところが、この対応は1対1ではない。なぜなら、明らかに$(\eta^1,\eta^2)$と$(\alpha\eta^1,\alpha\eta^2)\ (\alpha\in\mathbb{C})$は同じ$(x^1,x^2,x^3)$を与えるからである。そこで、この任意性を利用し、
\begin{align*}
\abs{\eta^1}^2+\abs{\eta^2}^2=r\label{norm}
\end{align*}
となるように$(\eta^1,\eta^2)$を規格化し、あらためて$\xi^{a}=\frac{\eta^{a}}{\sqrt{r}}\ (a=1,2)$とすると、
\begin{align*}
x^1
&=\xi^{1*}\xi^2+\xi^{2*}\xi^1\\
x^2
&=-i\xi^{1*}\xi^2+i\xi^{2*}\xi^1\\
x^3&=\abs{\xi^1}^2-\abs{\xi^2}^2
\end{align*}
が得られ、\eqref{q}式、\eqref{w}式、\eqref{e}式が再現される。
つまり、スピノル成分は3次元座標を平面に射影したときの、平面内の座標であると理解することもできる。
- ガンマ行列のエルミート性は、必須の条件ではない。 ↩︎
- 今はガンマ行列を最も小さいサイズ($2\times 2$)の行列として表現しているが、より大きいサイズで表現することも可能である。その場合、そのサイズのガンマ行列が作用するベクトル空間の元をスピノルと呼ぶ。つまり、ガンマ行列のサイズに応じてスピノルの次元も変わる。 ↩︎
- $n\times n$行列$M$の行列式が0であるということは、行列$M$の$i,j$成分$M_{ij}$を用いて、
\begin{align}
\sum_{i_1,i_2,\cdots,i_n=1}^{n}\varepsilon_{i_1i_2\cdots i_n}M_{1 i_1}M_{2 i_2}\cdots M_{n i_n}=0
\end{align}
と書ける。
一方、各成分を$M_{ij}=u_iv_j$と因数分解すれば、行列式は
\begin{align}
\sum_{i_1,i_2,\cdots,i_n=1}^{n}\varepsilon_{i_1i_2\cdots i_n}u_{1}v_{i_1}u_{2}v_{i_2}\cdots u_{n}v_{i_n}
\end{align}
となり、$u_{1}v_{i_1}u_{2}v_{i_2}\cdots u_{n}v_{i_n}$は$i_1,i_2,\cdots,i_n$のうちのどの1組を入れ替えても不変だから、これは恒等的に$0$である。したがって、行列式が$0$の行列は$M=uv^t$と、ベクトルのテンソル積として表せる。
ただし、この表し方は一意ではない。例えば、
\begin{align}
\mqty(6 & 4 \\ 3 & 2)=\mqty(2 \\ 1)\mqty(3 & 2)=\mqty(1 \\ \frac{1}{2})\mqty(6 & 4)=\cdots
\end{align}
のように、何か1つテンソル積での表し方を見つけたら、その縦ベクトルを$a$倍、横ベクトルを$\frac{1}{a}$倍したものも解になる。 ↩︎ - 右辺の$\frac{1}{2}$は$2\times 2$単位行列のトレースの値を打ち消すためのものである。 ↩︎
- 3次元回転のスピノルにおいては、$\zeta$と$\xi^{\dag}$が同じ変換性を示すことから、このようなことが可能となる。スピノルの変換性については、スピノルの座標変換で議論する。 ↩︎
- まだ左辺と右辺に1自由度の差があるが、これは位相の不定性として最後まで残ることになる。 ↩︎
- $e^{\frac{i}{2}\gamma}$の値は$0\leq\gamma <4\pi$で一巡するため、この範囲だけ考えればよい。 ↩︎
参考文献
- 物理学者のためのスピノル入門 http://phys.co-suite.jp/note.html 数学・物理学専門のインターネット家庭教師 物理・数学のノート
- 窪田高弘, 臨時別冊・数理科学SGCライブラリ-66 物理のためのリー群とリー代数, サイエンス社, 2008
- 和田純夫, 今度こそわかるシリーズ 今度こそわかるファインマン経路積分, 講談社, 2014


コメント